A few months ago bloggers argued about a parent who complained that the Common Core had needlessly complicated subtraction. The controversial techniques involve deconstructing “hard” numbers into “easy” numbers and working on the parts to get the answer. Most the teachers commented that the parent didn’t understand that the new method showed the deep meaning of the math. Most the parents said their children were frustrated and giving up.
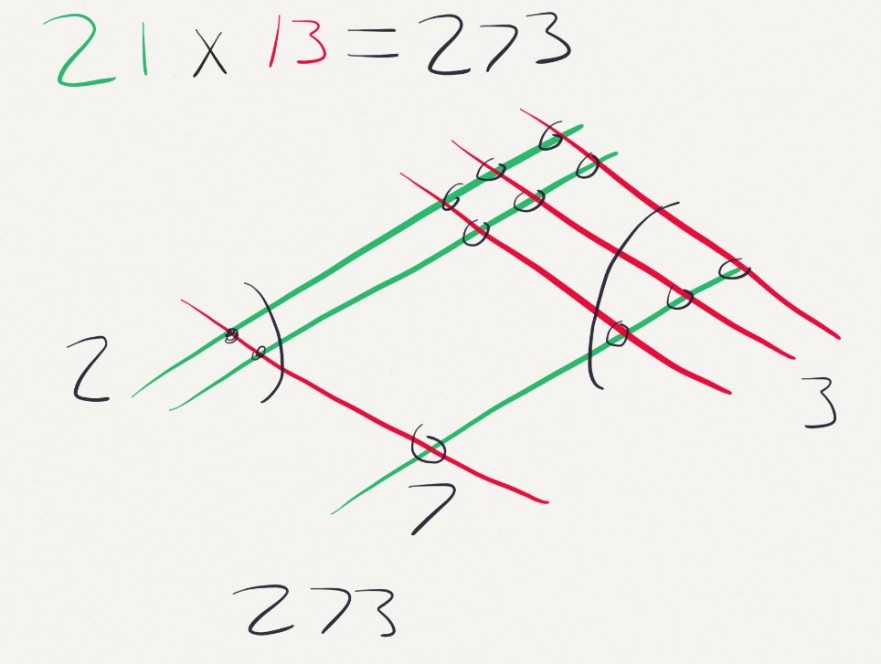
This week teachers and parents are posting a video on Facebook showing Chinese multiplication. The video and the picture above show that if you draw diagonally intersecting lines based on the numbers and count the intersections in the right order you can construct the right answer. Everybodysays it’s pretty cool. One friend, a really smart, really loud opponent of the Common Core, shared the video and commented, “This is awesome!”
That had me puzzled: Why the inconsistent responses to new ways to calculate, particularly from the Common Core opponent?
My first thought was that if you label something “Common Core” too many people will automatically defend it or reject it out of hand. (Which is true.) But then I realized that part of the issue lies in the claim that the criticized technique shows the deep meaning of subtraction. That claim is false. (No one that I’ve heard claims that Chinese multiplication shows the deeper meaning of multiplication.)
Regarding the deep meaning of subtraction, one asks: How far apart are two numbers? Period. To show the deeper meaning, look at where numbers fall on the number line. When you do that, you can see how far apart any two numbers are: natural numbers, whole numbers, integers, rationals, and irrationals. (You need a plane to show the distance between complex numbers.)
Deconstructing and working on the parts shows something else, and it can, in fact, be interesting and is a good way to do mental arithmetic. But to get to the interesting and practical, one has to have a foundation that doesn’t seem to have been built. If teachers presented the disputed subtraction method to students after they mastered the basics, it wouldn’t be frustrating and many might find it cool and useful.
Turning to multiplication, one asks: What happens when you combine groups? You can show thatwith manipulatives, drawings, and, of course, our friend the number line. You learn to multiply numbers with two or more digits by lining them up vertically by place value, multiply single digit numbers with the same place value, and then adding those results together. (In other words, you deconstruct, do the operations, and reconstruct.)
With those lines and dot-counting the Chinese method loses track of place values until the end and you don’t multiply or add anything. I don’t really know how practical it is, particularly for multi-digit numbers, but it is thought provoking to explore.
Back to the controversy. Teachers who want more support for Common Core Math need to be wise about when and how they present new techniques and contexts. Something like the subtraction and Chinese multiplication methods should come after they know their students have mastered working with multiple digit numbers. And to do that, teachers need to find and teach to mastery with the simplest techniques. Then, when students have mastered those, they will be ready for the enrichment.
And instead of saying, “Argghhhhh!” students may be saying, “Awesome!”
Sandy Merz
I grew up in Silver City, New Mexico and went the University of New Mexico, earning a Bachelor of Science degree in Geology. After working for the U.S. Geological Survey in remote regions of western New Mexico, I moved to Tucson to attend graduate school at the University of Arizona, earning a Master of Science degree in Hydrogeology. While working as an intern hydrologist for a local county agency, I started doing volunteer work that involved making presentations in schools. At that moment I knew teaching was the path to follow. It must have been a good decision because I’m still on the path after thirty-two years. My teaching certificates are in math and science and I am a National Board Certified Teacher in Career and Technical Education. After teaching engineering and math and elective classes at the same school in downtown Tucson my whole career, I've moved to a different middle school and district on the edge of town to teach math. In addition to full time teaching, I am actively involved in the teacher leadership movement by facilitating National Board candidates, blogging for Stories from School Arizona, and serving on the Arizona K12 Center’s TeacherSolutions team. In January 2017, Raytheon Missile System named me a Leader in Education and I'm a former Arizona Hope Street Fellow.
Comments 1
Hi, Sandy! Great post. I think that teaching math and preserving students’ “math attitude” is so important. Unfortunately, many adults struggle with low efficacy in math from their grade level experiences. Like many other school experiences, adults feel that they have the right to weigh in on teaching math because they have been on the student side of being taught math. It’s interesting when these issues become so convoluted with disagreement. You have really sorted it out in this post. I agree that students must understand the concepts before time-saving strategies are introduced. Once the fundamental concept is understood, a multitude of saving-strategies should be introduced and discussed so that students can choose strategies that will contribute to success and decreased anxiety manipulating numbers in the world.